Linear Regression

Regression (Regression toward the mean) 이란?
통계학에서 사용되는 용어로 관찰된 연속형 변수들에 대해 두 변수에 대한 추정 모델을 구한 뒤 분석하는 기법을 말합니다. 
데이터 관련 분야에선 작거나 큰 데이터가 나와도 해당 데이터들은 전체의 평균으로 회귀, 되돌아가려는 속성을 말합니다.

Linear Regression (선형회귀)란?
통계학에서 사용되는 용어로 종속 변수 y와 한개 이상의 독립 변수 x와의 선형 관계를 모델링하는 기법을 말합니다.
선형회귀는 가설함수(직선의 방정식)을 통해 해당 식을 구하며 알려지지 않은 변수를 데이터를 통해 추정합니다.
선형회귀는 머신러닝 분야에서 중요한 기법입니다.

선형회귀를 통해 데이터를 가장 잘  represent하는 최적의 직선의 방정식을 찾는 것이 목적입니다.

아래 그림을 보면 파란 점들과 빨간 직선이 있습니다.
파란 점들은 실제 데이터들이고 빨간 직선은 데이터들을 통해 모델링된 가설 함수이며 직선의 방정식입니다. 

출처: Wikipedia

 위 직선을 나타내는 직선의 방정식, 함수를 가설 또는 가설 함수(Hypothesis)라 하며 아래와 같이 나타냅니다.

Hypothesis

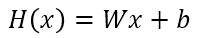
H(x)는 우리가 세운 가설 함수, 즉 데이터 x의 추정 값이며 기울기를 나타내는 W는 Weight, y절편을 나타내는 b는 bias입니다.

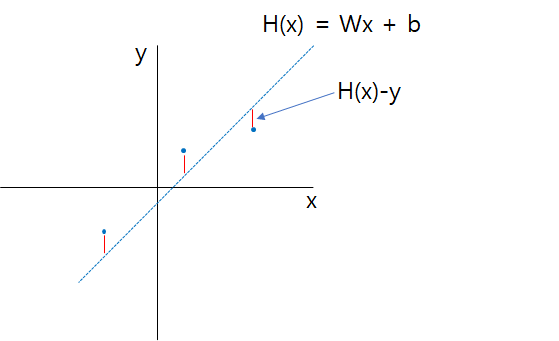
위 가설 함수는 3개의 데이터를 추정하여 만들어진 직선입니다.
가설 함수를 통해 얻을 수 있는 추정 값(H(x))과 실제 데이터(y) 값과의 차이 H(x)-y를 error, loss, cost라고 하며
당연히 error가 적을 수록 우리가 세운 가설 함수는 실제 데이터 예측에 대한 정확도가 높다는 뜻입니다.

따라서 선형 회귀의 목표는 
각 데이터와 추정값에 대한 error의 합이 최소가 되도록 하는 직선의 방정식 H(x)을 그리는 W와 b를 구하는 것입니다. 

하지만 단순히 H(x)와 y의 차의 합을 구하게 되면 의미가 없게됩니다.
그 이유는 error 값은 음수가 될 수 있기 때문에 대한 단순한 차에 대한 합은 정확하지 않습니다.

따라서 우리는 error 값을 제곱하여 평균을 구합니다. 
이 평균을 구하는 함수를 비용 함수라 하며 아래와 같이 정의할 수 있습니다.

비용 함수 Cost(W,b)

모든 에러의 제곱을 더한 뒤 데이터의 개수만큼 나눕니다.
이 값이 최소가 되도록 하는 W, b를 각 기울기, y절편으로 갖는 직선의 방정식을 구하는 것이 선형 회귀의 목적입니다.