[문제]
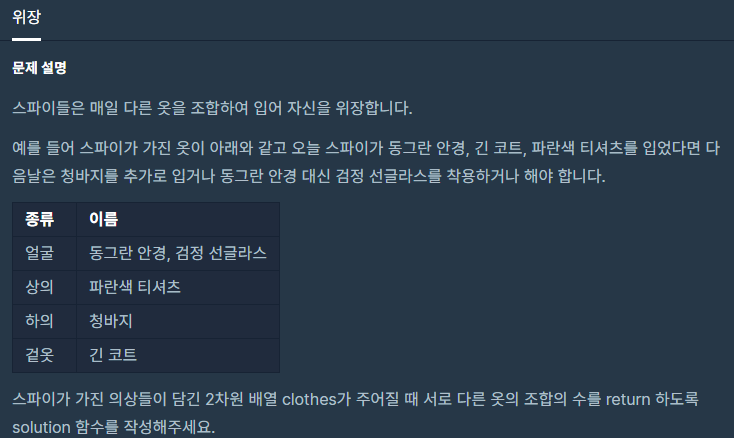
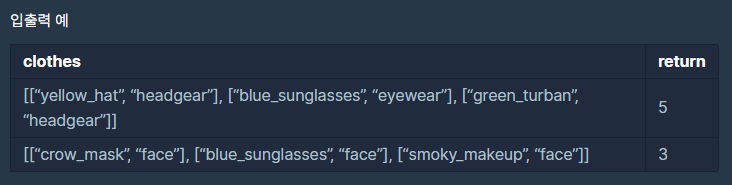
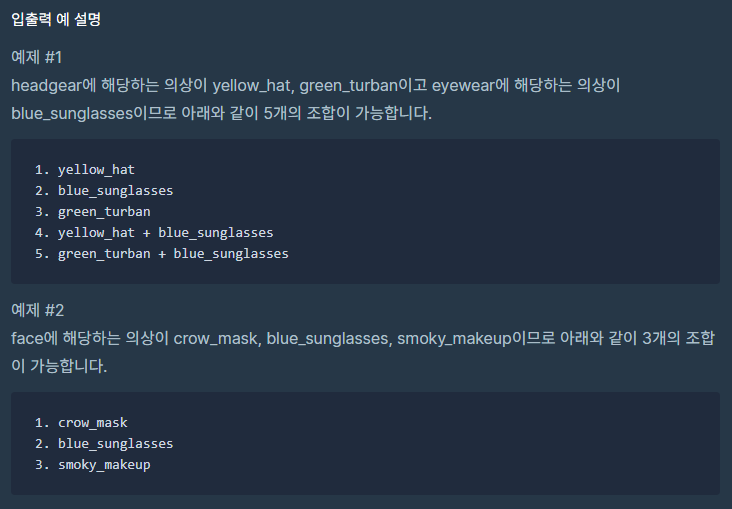
문제는 우선 간단하다. 얼굴, 상의와 같은 종류의 의상들이 주어지는데 그들 중 최소 1개 이상의 조합의 가지수를 구하는 것이다. 물론 같은 종류의 의상은 중복으로 착용할 수 없다. 예제를 살펴보면 첫 번째 예제의 경우 headgear 종류의 의상이 2개 eyewear에 해당하는 의상이 1개이므로 총 2개의 종류와 의상의 개수는 3개이다. 따라서 1개의 조합, 2개의 조합으로 입을 수 있으며 총 5가지의 수가 나온다.
[풀이]
우선 해시맵을 이용하여 key-value 쌍을 (종류-의상들)로 저장한다. 예를 들면 "face" - ["crow_mask, "blue_sunglasses, ...]와 같은 식이다. 이렇게 분류한 뒤 종류 별로 조합하여 가능한 경우의 수를 모두 구하면 된다. 이 부분이 핵심인데, 기존에 내가 생각했던 방법은 너무 복잡하여 구글링을 해 보았다.
그 결과 상당히 간단한 식을 얻을 수 있었다. 고등학교 때, 경우의 수 관련된 부분에서 배웠다고 하는데 가물가물하다. 우선 첫 번째 예제로 예를 들면, headgear - 2개, eyewear - 1개 중 최소 1가지부터 최대 2가지를 입는 경우의 수를 구하면 다음과 같다.
(2+1) * (1+1) - 1 = 5
두 번째 예제로 하면 (3+1) - 1 = 3
즉, 각 종류별 의상의 개수를 a,b,c라고 하면 모든 경우의 수는 (a+1)*(b+1)*(c+1) 이다. 여기서 하나도 선택하지 않는 경우의 수 1개를 빼주면 된다. 해당 공식은 5개의 수로 3자리 숫자를 만드는 것과 비슷한 것 같다. 5개의 수를 공용으로 사용하여 3자리 수를 만드려면 1개씩 덜 사용하여 5x4x3인데, 해당 문제에선 의상 종류가 분리되어 있으므로 1개씩 덜 사용할 필요가 없으므로 a*b*c이다. 그런데 여기서는 각각의 의상을 선택하지 않을 경우의 수를 1씩 더해주어야 한다고 한다. 이 부분이 살짝 이해가 안간다.. 어쨌든 이러한 공식으로 모든 테스트 케이스가 통과가 되었다. 정확한 이해가 가지 않아 찜찜하다.
[코드]
#include <string>
#include <vector>
#include <unordered_map>
using namespace std;
int solution(vector<vector<string>> clothes)
{
int answer = 1;
// 해시맵에 종류별로 추가 (종류-이름)
unordered_map<string, vector<string>> map;
for(const auto& vec : clothes)
{
map[vec[1]].push_back(vec[0]);
}
size_t typeNum = map.size();
// i.e.
// face - ["crow_mask", "blue_sunglasses", "smokey_makeup"]
// 종류가 1가지면 의상의 개수를 반환합니다.
// 잘 이해가 가지 않는 조합 경우의 수
for(const auto& pair : map)
{
answer *= pair.second.size() + 1;
}
// 모두 입지 않을 경우의 수를 하나 빼준다고 한다.
--answer;
return answer;
}'Algorithm > 프로그래머스' 카테고리의 다른 글
| [Level 2] 큰 수 만들기 (0) | 2021.09.20 |
|---|---|
| [Level 2] 점프와 순간이동 | C++ (0) | 2020.09.23 |
| [Level 2] 소수 찾기 - 완전 탐색 | C++ (0) | 2020.05.26 |
| [Level 2] H-Index - 정렬 | C++ (0) | 2020.05.24 |
| [Level 3] 베스트 앨범 - 해시 | C++ (0) | 2020.05.23 |





댓글