반응형
- 문제
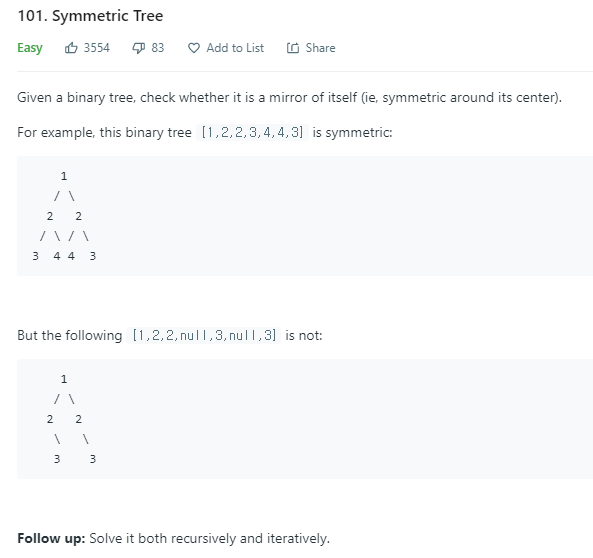
주어진 이진 트리가 중심을 기준으로 대칭인지 판별한다.
- 풀이
다른 여러가지 방법이 있겠지만, 내가 풀이한 방법은 다음과 같다.
1. root 노드를 기준으로 왼쪽 서브트리는 전위 순회(preorder)를 한 결과를 vector에 순서대로 저장한다.
2. root 노드를 기준으로 오른쪽 서브트리는 root-right-left 노드 순으로 순회한 결과를 vector에 순서대로 저장한다.
3. 위에서 구한 두 vector의 요소를 서로 비교하여 다른 요소가 있다면 false를 반환, 모두 같으면 true를 반환한다.
아래 코드에서 1번 예제인 [1, 2, 2, 3, 4, 4, 3] 트리를 예를 들어 위 방법을 적용해보면 다음과 같다.
1. leftSubTree: [2, 3, 4]
2. rightSubTree: [2, 3, 4]
3. 각 요소가 모두 동일하므로 true
2번 예제.
1. leftSubTree: [2, null, 3]
2. rightSubTree: [2, 3, null]
3. 동일하지 않은 요소가 있으므로 false
vector를 구하기 위해 왼쪽 서브트리와 오른쪽 서브트리를 모두 탐색하므로 O(n)의 시간 복잡도에 두 벡터를 비교하는 연산까지 하여 총 O(n)의 시간 복잡도를 가진다.
/*
[Easy] 101.Symmetric Tree
---------------------------------------------------------------------------------------------------------------------------------------------
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).
For example, this binary tree [1,2,2,3,4,4,3] is symmetric:
1
/ \
2 2
/ \ / \
3 4 4 3
But the following [1,2,2,null,3,null,3] is not:
1
/ \
2 2
\ \
3 3
---------------------------------------------------------------------------------------------------------------------------------------------
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution
{
public:
bool isSymmetric(TreeNode* root)
{
if (!root)
return true;
else if (!root->left && !root->right)
return true;
else if (!root->left)
return false;
else if (!root->right)
return false;
vector<TreeNode*> leftSubTree;
vector<TreeNode*> rightSubTree;
leftSubTree.reserve(400);
rightSubTree.reserve(400);
TraversingPreOrder(root->left, leftSubTree);
TraversingReverseOrder(root->right, rightSubTree);
auto size = leftSubTree.size();
if (size != rightSubTree.size())
{
return false;
}
for (auto i = 0; i != size; ++i)
{
if (!leftSubTree[i] && !rightSubTree[i])
{
continue;
}
else if ((!leftSubTree[i] || !rightSubTree[i]) || (leftSubTree[i]->val != rightSubTree[i]->val))
{
return false;
}
}
return true;
}
// root-left-right
void TraversingPreOrder(TreeNode* start, vector<TreeNode*>& leftSubTree)
{
if (start)
{
leftSubTree.push_back(start);
TraversingPreOrder(start->left, leftSubTree);
TraversingPreOrder(start->right, leftSubTree);
}
else
{
leftSubTree.push_back(nullptr);
}
}
// root-right-left
void TraversingReverseOrder(TreeNode* start, vector<TreeNode*>& rightSubTree)
{
if (start)
{
rightSubTree.push_back(start);
TraversingReverseOrder(start->right, rightSubTree);
TraversingReverseOrder(start->left, rightSubTree);
}
else
{
rightSubTree.push_back(nullptr);
}
}
};'Algorithm > LeetCode' 카테고리의 다른 글
| [Easy] 338. Counting Bits (0) | 2021.09.26 |
|---|---|
| [Easy] 121. Best Time to Buy and Sell Stock (0) | 2021.09.26 |
| [Easy] Leetcode | 70. Climbing Stairs | Dynamic programming (0) | 2020.04.20 |
| [Easy] Leetcode | 53. Maximum Subarray | dynamic programming (0) | 2020.04.18 |
| [Easy] Leetcode | 21. Merge Two Sorted Lists | Linked list (0) | 2020.02.01 |






댓글